引言

近日，荷兰代尔夫特理工大学Srijit Goswami团队在《自然》中发表最新研究成果，基于二维电子气上串联的半导体-超导复合广东会点阵列成功构筑了三格点的Kitaev 链，并通过对链上各点进行直接隧穿谱测量，首次在实验上演示Kitaev链上边缘零能马约纳拉束缚态（MBS）的鲁棒性和系统体态激发能隙的关联。

 第一章 背景介绍

近些年，随着人们对凝聚态拓扑结构研究的深入，有效构筑对外界干扰具有强鲁棒性的非平庸广东会相成为了当下的研究热点。  特别是一维拓扑超导体的实现，因为它可以构筑由Kitaev链模型所预言的马约拉纳束缚态(MBS)。因为这些零能边界态在能谱上被体态的激发能隙所隔离，所以可以避免局部扰动对它的影响，这一本征特性源于拓扑结构的“体边对应关系”。与此同时，受拓扑保护的MBSs也为拓扑广东会计算的实现提供物理载体。为此，人们最初尝试通过诱导半导体与超导复合纳米线的拓扑超导相变来构筑MBSs，但在这些纳米线系统中微观无序的噪声使得研究变复杂，从而无法验证线两端拓扑零能边界态的真实存在。正因如此，研究人员拟采取另一种方式来模拟MBSs，即通过调控原子链或半导体-超导复合体系中广东会点阵列来直接构建Kitaev链，并以此模拟非平庸超导零能模。基于纳米线和二维电子气(2DEG)系统实验上已经构建了两个广东会点的Kitaev链。然而，在双格点链中，两个广东会点均无法对应于系统体态。三广东会点链作为可以明确区分承载MBSs的边缘（外侧广东会点）与体态（中间广东会点）的最小单元，尽管近期研究在此类系统中观测到了稳定的零能态，但未能对中间广东会点的态密度进行深入研究。

本研究在InSbAs二维电子气中实现了三广东会点Kitaev链，并对链的体态与边缘态进行了系统研究。实验上，每个广东会点上的欧姆接触能够方便三个位点态密度的直接探测。通过调控广东会点间耦合强度和超导相位差，该研究成功在边缘广东会点诱导出鲁棒的零偏压电导峰(ZBPs)。实验证实，这些边缘相关的ZBPs总伴随着中间广东会点的激发能隙——该能隙可通过调节超导体间的相位差精确控制，从而明确建立了孤立零能边缘态与其抗局域扰动鲁棒性之间的关联。 

第二章 广东会点阵列Kitaev链模型介绍

在广东会点阵列上实现Kitaev链需要精确调控各广东会点的电化学势能（μ_i）及其相邻位点间的耦合强度（t, Δ），具体可以通过调节自旋极化的广东会点与半导体-超导体异质结中的Andreev束缚态之间的耦合来实现。因为该体系中存在两种关键相互作用：由弹性共隧穿(ECT)而产生的跃迁作用(t)，以及由交叉Andreev反射(CAR)作用产生/湮灭超导复合纳米线中库珀对而产生的配对作用(Δ)。本征自旋-轨道耦合使得相同自旋邻位点间可发生CAR，或相反自旋邻位点间发生ECT——这些过程在自旋守恒条件下本应被禁止。当各广东会点的塞曼能(E_z>>t,Δ)足够大时，在电荷简并点处多广东会点阵列可以等效为一维自旋极化链，从而完美模拟Kitaev模型。

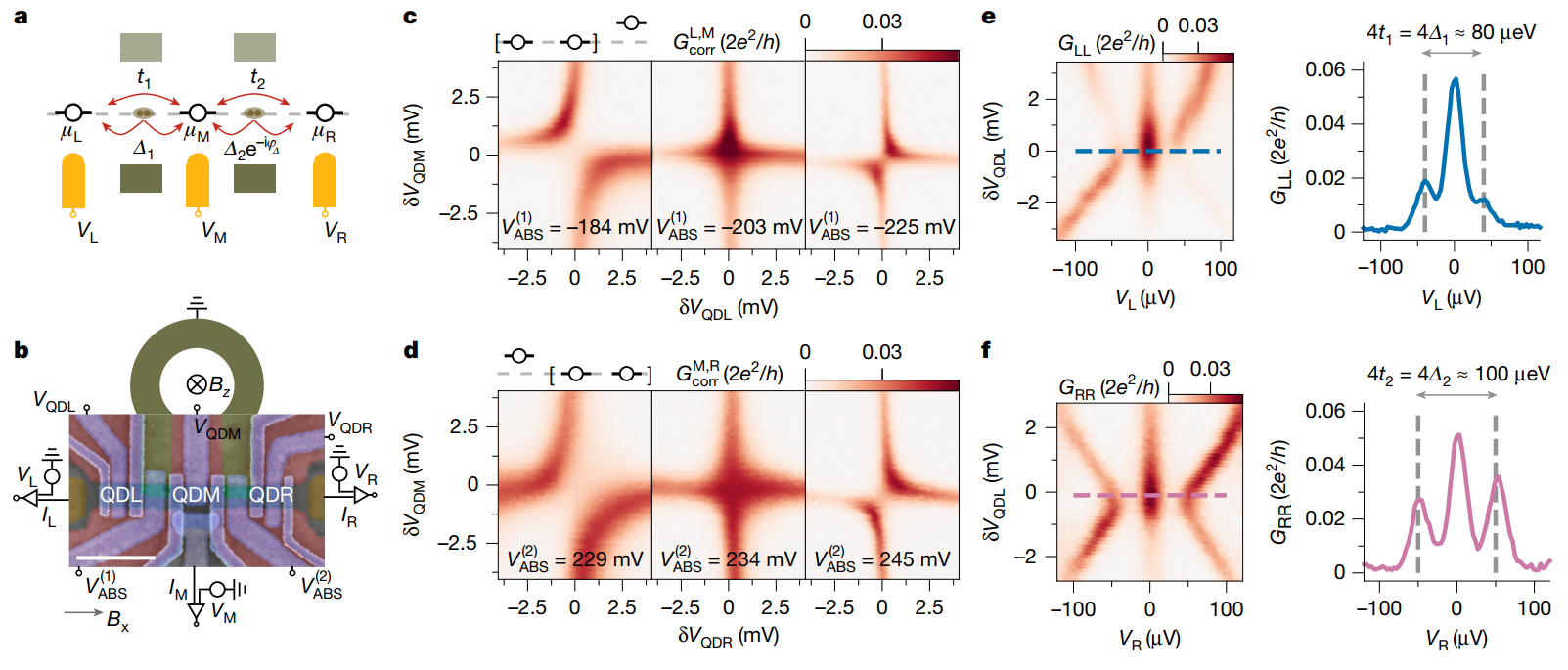
图1 (a)展示了基于耦合三广东会点阵列Kitaev链的能级示意图，以及点间之间的相互作用示意图。(b)实验上三广东会点阵列的扫描电镜图（SEM），其中相邻超导复合区域的相位差通过调节外接环的穿透磁通来控制。(c)在不同的超导栅控电压下V_ABS^（1），左边和中间广东会点的关联电导G_corr^L,M随广东会点电压δV_QDL和δV_QDM的变化。（d）在不同的超导栅控电压下V_ABS^（2），中间和右边广东会点的关联电导G_corr^M,R随广东会点电压δV_QDM和δV_QDR的变化。(e) 左边广东会点的偏压电导谱G_LL随外接偏压V_L和点栅控电压δV_QDL的变化，右边子图展示在δV_QDL=0下基于电导谱信号确定左边和中间广东会点间ECT 和CAR强度。（f）右边广东会点的偏压电导谱G_RR随外接偏压V_R和点栅控电压δV_QDR的变化，右边子图展示在δV_QDR=0下基于电导谱信号确定中间和右边广东会点间ECT 和CAR强度。

图1.(a)展示了耦合三广东会点阵列的能级示意图，其中μ_i (i=L,R,M) 代表着各个广东会点的在位能，可以通过调节相应广东会点的栅压V_QDi来控制。Δ₁ (Δ₂) 和t₁ (t₂) 代表着广东会点QD_L (QD_M) 和QD_M (QD_R) 之间CAR和ECT的幅度。实验上，相邻点间ECT和CAR强度可以通过超导区域安德烈夫束缚态（ABS）的栅控电压V_ABS⁽¹⁾和 V_ABS⁽²⁾来控制，相邻超导体内库珀对的相位差可以通过外接环的穿透磁通来调节，参见图1.（b）。MBSs的构筑要求广东会点阵列处于最佳（Sweet point）工作区域，即每个广东会点的化学势位于费米能级（μ_i = 0），并且相邻点间的ECT 和CAR具有相同强度。

为了确定ECT和CAR达到平衡时的条件，具体研究在不同ABS调控电压下相邻广东会点间的关联电导信号G_corr^L,M和G_corr^M,R随点调控电压的变化，具体参见图1.（c）和（d）。当且仅当相邻点间ECT和CAR的强度相等时，关联电导信号在二维参数空间的变化模式呈十字形状，由此确定实验上V_ABS^（1）和V_ABS^（2）的工作数值。为了进一步确定点间相互作用强度的具体数值，实验上测量了平衡条件下左、右广东会点的微分电导谱信号随局部偏压VL,R的变化，具体根据零偏压电导峰两侧偏锋之间的距离来确定ECT和CAR的强度，参见图1.(e)和（f）。

 第三章 相位调控和体态的激发能谱

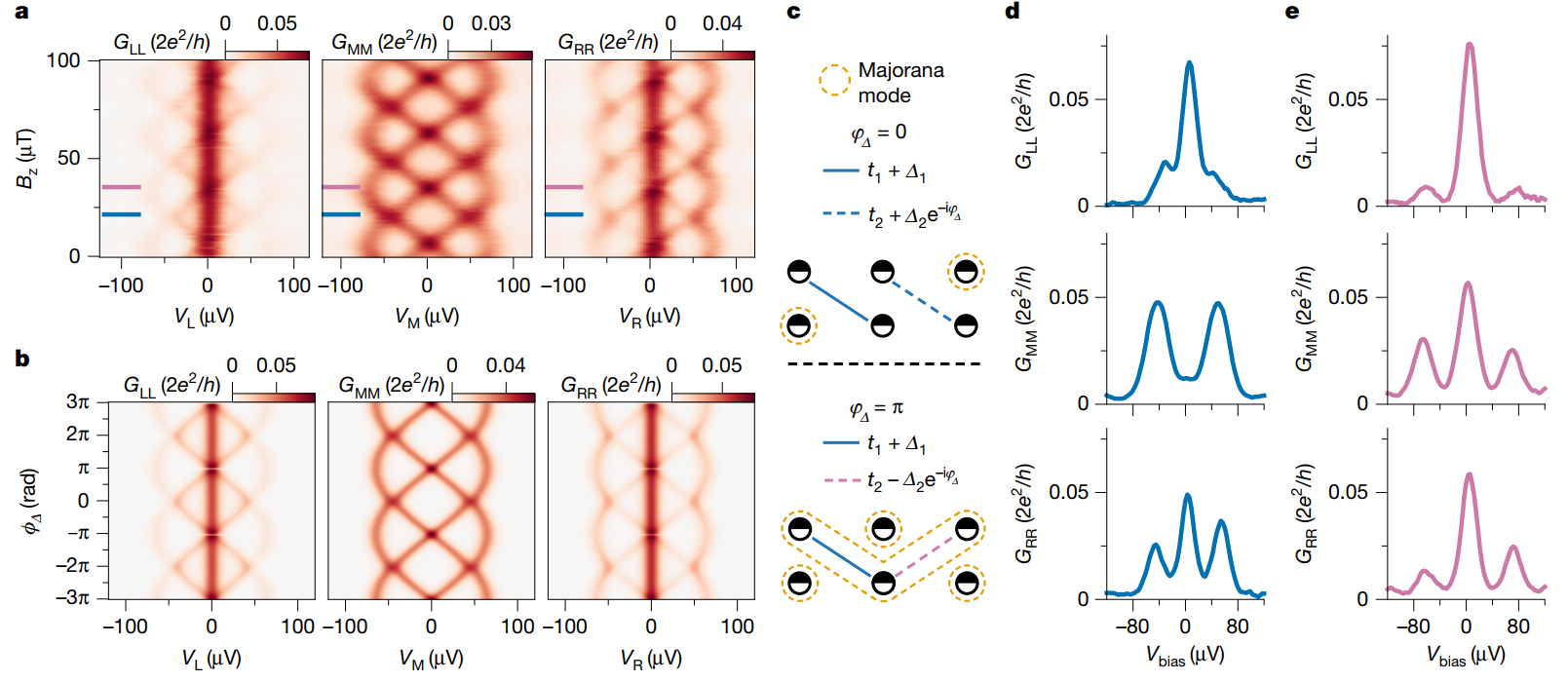
图2 (a)展示当超导复合广东会点阵列处于ECT和CAR平衡条件下，实验上各点位局部电导测量信号（G_LL,G_MM,G_RR）随外部施加磁场强度BZ和广东会点偏压(V_L,V_M,V_R)的变化。(b)根据广东会点阵列实际的参数，各点局部电导信号随偏压和穿透磁通相位变化的理论模拟数据图。（c）当穿透磁通相位Φ_Δ=0和 π时，广东会点阵列在马约纳拉表相下的连接模型示意图。（d）依据实验测量数据图(a)展示当Φ_Δ=0时，广东会点阵列上各点的局部电导信号随相应偏压的变化。（e）展示当Φ_Δ=π时，各点局部电导信号随相应偏压的变化。

当相邻广东会点之间的ECT和CAR处于平衡条件（sweet point）时，三格点Kitaev链的状态可以通过改变广东会点中间超导体的相位来进行有效调节。实验上，通过测量每个格点处电导信号（G_LL,G_MM,G_RR）随外界施加磁场强度 Bz和局部偏压(V_L,V_M,V_R)的变化来反映超导相位差对系统边界态的影响，具体请参见图2.（a）。具体而言，零偏压电导峰（ZBP）的出现则意味着局部束缚态的存在。从实验测量数据图可以判断，左、右两端广东会点处存在着稳定的零能局部束缚态，不会随两端超导连接区域库珀对的相位差Φ_Δ变化。相反，中间广东会点的零偏压电导峰信号呈周期变化的趋势。 只要当相位Φ_Δ（mod 2π）=π时，ZBP才会存在于中间格点，详情请参见图2. (e)。但对于三格点的Kitaev链，中间广东会点作为构成系统体态的核心部分，该点位零能束缚态的存在则意味着体系此时不存在体态能隙。当相位Φ_Δ取其他数值时，G_MM 则不再存在着零偏压电导峰。 例如，图2.（d）展示了当Φ_Δ（mod 2π）=0, 广东会点阵列各格点局部电导信号随相应偏压的变化。此时，相比于左、右两端格点的边界态，中间格点ZBP的消失则说明体系存在体态能隙。

理论上，磁通相位的改变作用可以转化为中间与右端格点间CAR作用强度Δ₂的调制，在马约纳拉表象（Majorana basis）下进而重现实验上的测量数据，参见图2.（b）。基于此理论，研究人员同时还可以确定当超导相位Φ_Δ取不同值时，零能束缚态在马约纳拉表象下的空间分布。相比于Φ_Δ=0的情形（只存在一对局部零能束缚态），当Φ_Δ=π广东会点阵列出现在四个束缚态，详情参见图2.（c）。

第四章 马约纳拉波函数的移动

图3 (a)当超导调节相位Φ_Δ=0时， Kitaev链各点位电导信号（G_LL,G_MM,G_RR）随左侧广东会点失谐量δV_QDL和局部偏压(V_L,V_M,V_R) 的变化。(b)展示（a）图中局部偏压等于零时，各点位电导信号随δV_QDL的变化。（c）表示当δV_QDL=0 mV 和-3 mV时，Kitaev链上零能束缚态的空间分布，以及在Majorana 表象下链各点位的连接模式。（d）当超导调节相位Φ_Δ=π时，链各点位电导信号随局部电压失谐量δV_QDL和相应偏压的变化。（e）展示（d）图中局部偏压等于零时，各点位电导信号随δV_QDL的变化。（f）与（c）图类似，展示当Φ_Δ=π时，Kitaev链上零能束缚态的空间分布，以及在Majorana 表象下链各点位的连接模式。

与此同时，超导连接区域相位差的调节也会影响零能束缚态在广东会点Kitaev链上的位置滑移。图3.（a）展示了当超导相位Φ_Δ=0时，各点位电导峰随左侧广东会点失谐量δV_QDL和局部偏压（V_L,V_M,V_R）的变化，其中零偏压电导峰（ZBP）随δV_QDL的变化反映了零能束缚态的演变。相比于位于右端ZBP，详见图3.（b）,位于链左端和中间的ZBP会随着δV_QDL变化。当广东会点栅控电压从-3mV调制0mV时，左端的ZBP 会出现，中间的ZBP 会消失。这也就说明了位于链中间格点的能量束缚态会随着δVQDL的增大转移至左端格点，参见图3.（c）。但当超导相位Φ_Δ=π时，图3.（d）显示除了最左端的电导信号，中间和右端的零偏压电导信号不会随着δV_QDL的调节而发生变化。图3.（e）具体展示了零偏压下各点位电导信号随δV_QDL的变化。此时， 广东会点链上各格点零能束缚态的演变如图3.（f）所示。理论上，广东会点Kitaev链上零能束缚态随δV_QDL和Φ_Δ的空间转移可以通过Majorana表象下相邻点位间的连接方式来说明，具体请参见图3（c）和3（f）的格点连接图。

第五章 平衡点之外的零偏压电导峰

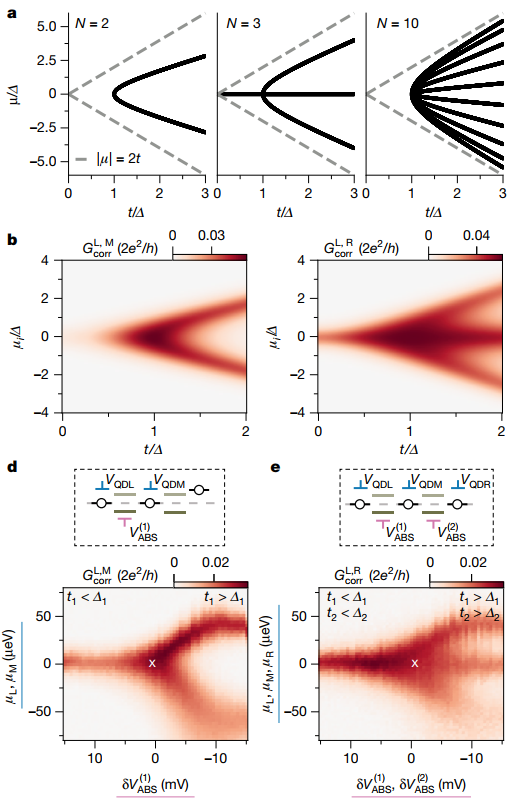
图4(a) 随着Kitaev链格点数目的增加，理论计算零偏压电导峰（ZBP）在t-μ 参数空间出现的区域。(b) 左图：展示基于两格点Kitaev 链，左端和中间广东会点的关联电导信号G_corr^L,M随ECT 强度t和各点位化学势μ变化的理论模拟计算图。右图：展示基于三格点Kitaev链，左、右两端广东会点关联电导信号G_corr^L,R随t和μ变化的理论模拟计算图。 （d）实验测量两格点Kitaev链关联电导G_corr^L,M随一支ABS的栅压δV_ABS⁽¹⁾和广东会点化学势μ_L和μ_M的变化，并且展示平衡点处各点位能级调控示意图（见方框图）。（e）实验测量三格点Kitaev链关联电导G_corr^L,R随ABS的失谐量（δV_ABS⁽¹⁾，δV_ABS⁽²⁾）和广东会点化学势（μ_L，μ_M，μ_R）的变化，并且方框图内展示平衡点处各点位能级结构。

相关理论研究表明，随着Kitaev 链格点数目N的增多，链的非局域本征零能解也就越多，如图4.（a）所示。当N=2时，链的零能解在t-μ 参数空间内是一条二次抛物线。当N=3时，除了抛物线，参数空间内μ=0的直线也对应着稳定的零能解。当N进一步增大，本征零能解的数目将布满整个非平庸参数空间（参见最右边子图）。在输运研究领域，Kitaev链本征零能解可以通过链两端的关联电导信号的峰值来体现。图4.（b）分别模拟了双格点链和三格点链的两端关联电导信号G_corr^L,M和G_corr^L,R在相应参数空间的分布。基于此，图4.（d）和4.（e）分别展示了双格点和三格点广东会点Kitaev链纳米器件的实际测量关联信号，随超导连接区域ABS 态的失谐能量（δV_ABS⁽¹⁾，δV_ABS⁽²⁾）和广东会点化学势（μ_L，μ_M，μ_R）的变化。实验测量结果与理论分析的相匹配验证了增加Kitaev链的长度能增加零能模式的数目，从而凸显长Kitaev链在非平庸零能模式调控的优势。

终章 总结

该项工作通过将三个广东会点阵列用两个半导体-超导区域耦合，实现了三站点Kitaev链。研究发现超导体间相位差的调控，会影响相邻广东会点间CAR耦合的相对相位，从而决定了系统的能谱结构。这一发现对研究更长链中的零能模尤为重要。通过精确调控相位，研究人员证明外侧广东会点出现零偏压峰（ZBP）的同时，中间广东会点会伴随激发能隙，这证实了零能模局域在链端的特性。我们进一步表明，通过调节广东会点能级失谐度，可实现马约拉纳波函数权重在不同位点间的平滑转移。这种马约拉纳束缚态（MBS）的空间操控技术，是基于门电路编织方案实现马约拉纳广东会比特 的核心要求。总体而言，我们的实验数据在广泛参数范围内与Kitaev模型预测高度吻合，为需要可靠方法制备强健局域马约拉纳束缚态的研究迈出了重要一步。

参考文献

ten Haaf, S.L.D., Zhang, Y., Wang, Q. et al. Observation of edge and bulk states in a three-site Kitaev chain. Nature (2025).

DOI: https://doi.org/10.1038/s41586-025-08892-5

撰稿｜刘志海