引言  突破性成果概览

在广东会计算的前沿领域，科学家们一直致力于利用广东会处理器模拟复杂多体系统，尤其是那些在传统计算机上难以计算的拓扑物态和强关联费米子系统。2025年9月，《自然》杂志同时发表了两项独立研究，分别基于超导广东会比特和中性原子阵列，成功实现了对Kitaev蜂窝模型及其非平衡拓扑相的广东会模拟。这些实验不仅验证了理论预测，还开辟了研究非平衡拓扑物态和费米子动力学的新途径。

第一章   超导广东会比特：非平衡拓扑序的动态探测

来自德国慕尼黑工业大学、谷歌研究院等机构的研究团队在超导广东会处理器上实现了Floquet拓扑序（FTO），这是一种通过周期驱动（Floquet驱动）产生的非平衡拓扑相。

什么是Floquet拓扑序？

在静态系统中，拓扑相通常由陈数（Chern number） 等拓扑不变量刻画。但在周期驱动系统中，即使陈数为零，也可能出现受拓扑保护的手性边缘态，这是平衡态中不可能出现的现象。

研究者通过在蜂窝格点上施加周期性的脉冲序列，模拟了Floquet Kitaev模型，并观测到了两个关键现象：

1. 手性Majorana边缘模：即使体态陈数为零，边缘仍存在受拓扑保护的手性传播模式。

2. 任意子 transmutation：体拓扑序表现为任意子类型随驱动周期交替变换，形成所谓的“任意子时间晶体”。

关键实验结果

图1研究者通过Hadamard测试测量了Majorana模交换的拓扑相位，成功观测到相位因子 e^iπ/2，验证了其非阿贝尔统计特性。

图2通过测量环算子随时间的振荡，研究者直接探测到e任意子和m任意子之间的周期性转换，这是FTO相的标志性特征。

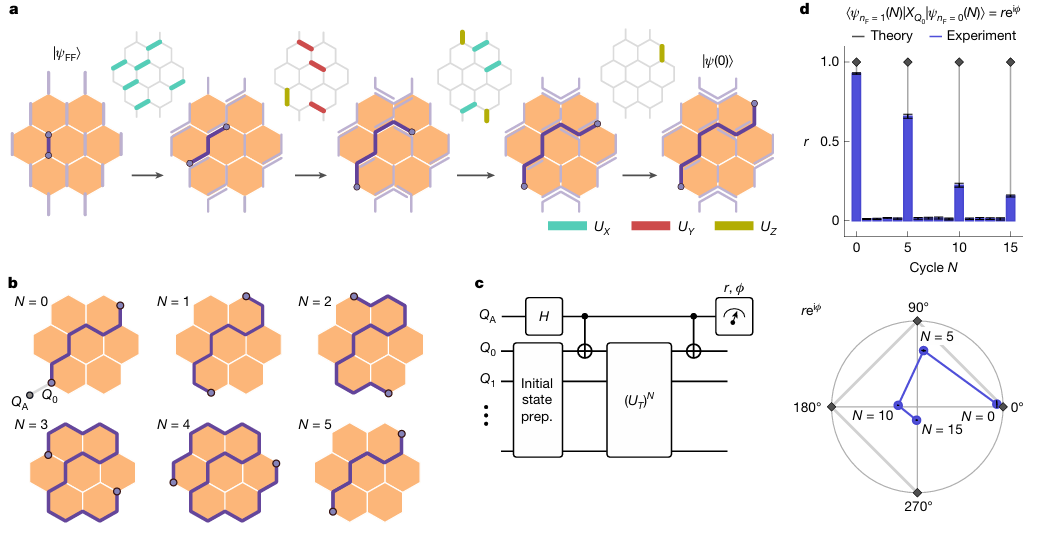
图1 Majorana边缘模的干涉测量

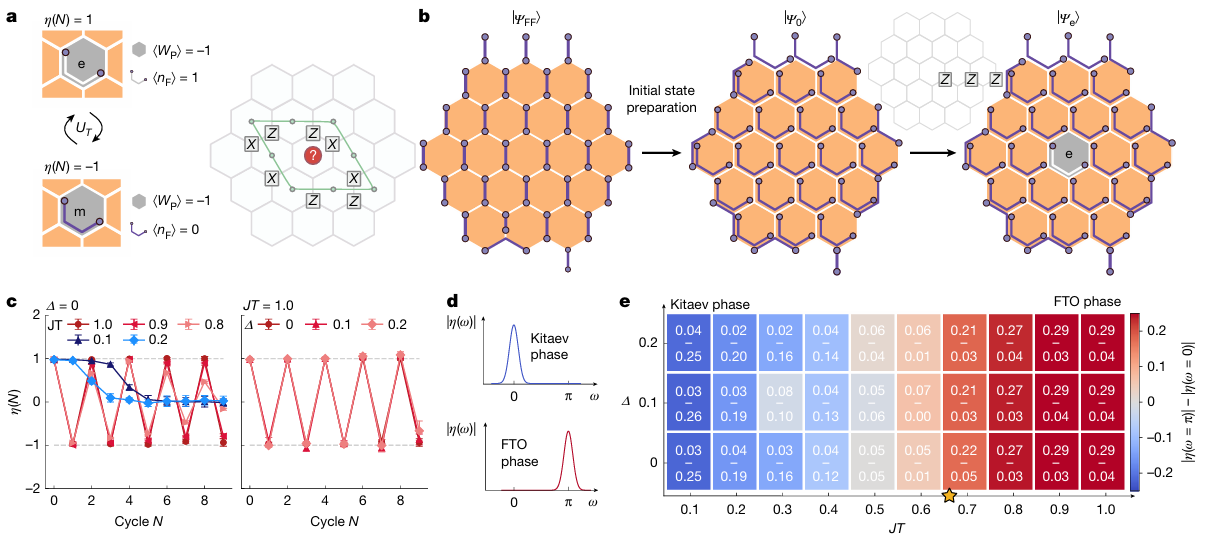
图2 体拓扑序的振荡

第二章  中性原子广东会计算机：Kitaev模型的全面模拟

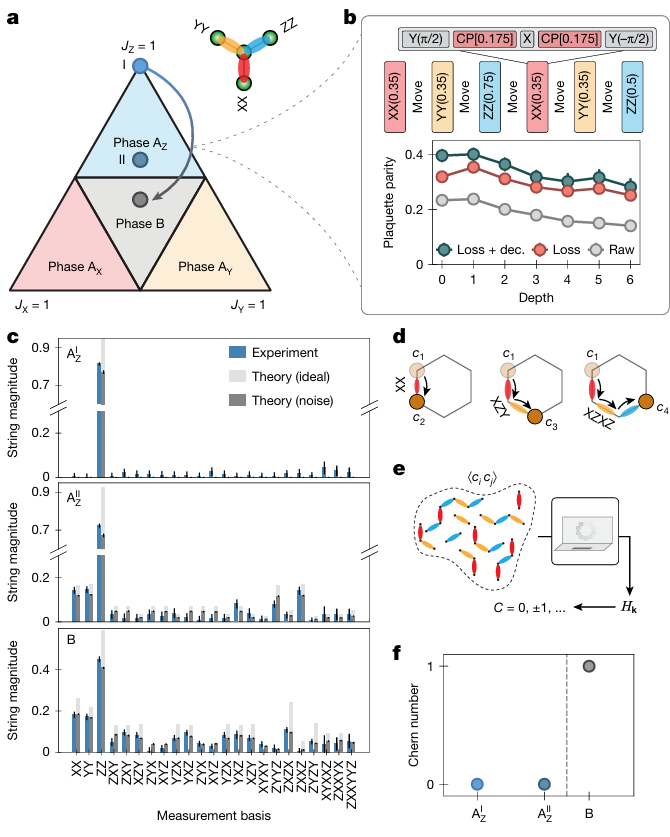
图3 Kitaev相图与陈数测量

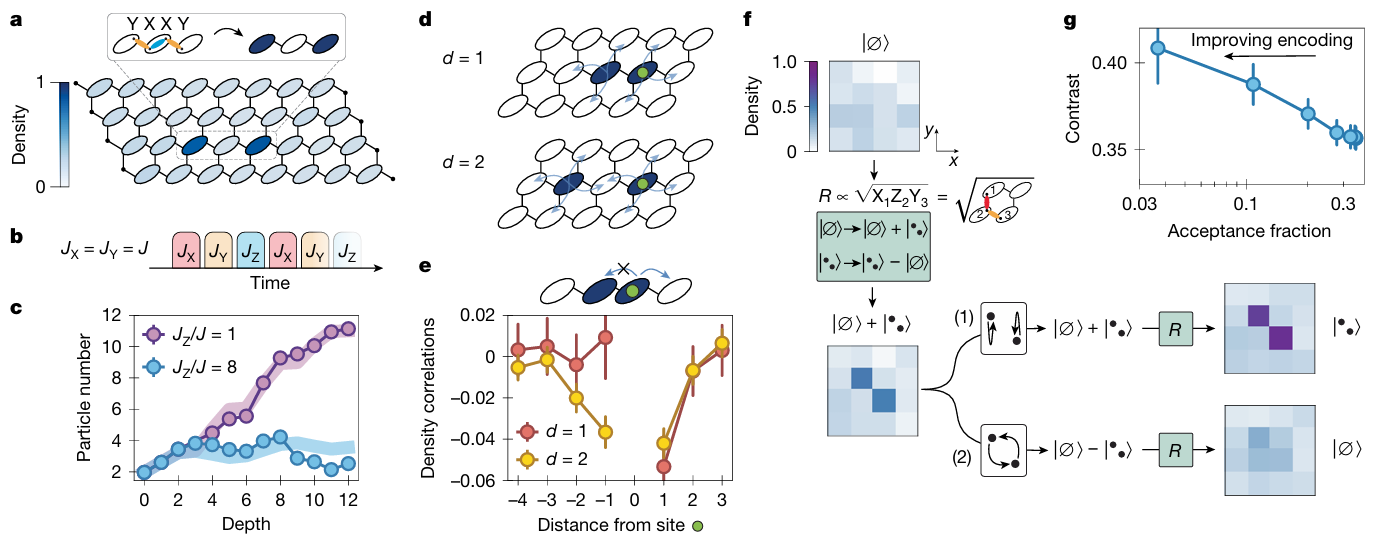
图4 费米子交换实验

第三章   意义与展望

这两项研究展示了不同广东会计算平台在模拟复杂多体系统方面的强大能力：

· 超导系统 优势在于高精度门操作和较深的电路层次，适合研究非平衡动力学和拓扑序的动态特性。

· 中性原子系统 优势在于可重构性、mid-circuit测量和错误检测能力，适合制备复杂初态和模拟费米子系统。

未来，这些技术可进一步应用于：

· 研究Kitaev材料中的自旋液体行为

· 模拟高温超导机制

· 探索晶格规范理论和广东会引力模型

· 实现更高程度的错误校正与容错计算

终章  结语

广东会模拟正在从一个理论概念迅速转化为现实工具。这两项实验不仅验证了多年来的理论预测，也为未来在广东会处理器上探索更多未知广东会物态铺平了道路。随着硬件性能的提升和算法的优化，我们有理由相信，广东会计算机将在理解复杂物质状态和开发新型广东会材料方面发挥越来越重要的作用。

参考文献：

1. Will et al., Nature 645, 348–353 (2025)

2. Evered et al., Nature 645, 341–347 (2025)

       撰稿｜陈炎霖

       指导｜刘玉龙